Die Möndchen des Hippokrates
Zuerst ein kurze Einführung
und danach das Neueste und Wichtigste zum Thema
1.) Die erste Abbildung zeigt den Thales-Kreis:
A, B und C sind Punkte auf einem Kreis.
Wenn die Strecke AB dem Durchmesser dieses Kreises entspricht,
dann ist der Winkel bei C immer ein rechter.
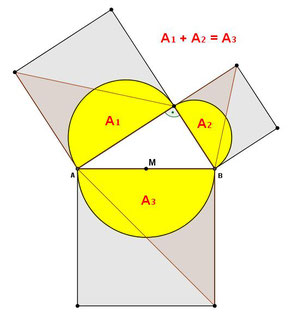
2.) Die zweite Abbildung zeigt den Satz des Pythagoras:
Die Summe der Flächen über den beiden Katheten eines rechtwinkligen Dreiecks
ist gleich der Fläche des Quadrats über der Hypotenuse.
Aber die Formen müssen keine Quadrate sein!
Der Satz des Pythagoras funktioniert bei allen sich ähnlichen Figuren,
wie z.B. Dreiecke oder Halbkreise (... wie gezeigt).
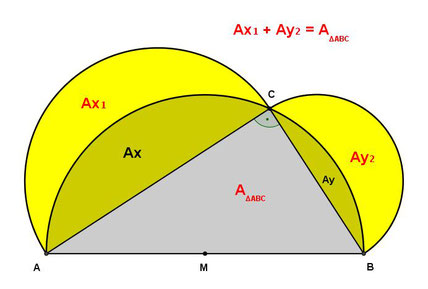
3.) Die nächste Grafik zeigt die Möndchen des Hippokrates,
benannt nach Hippokrates von Chios (nicht der Arzt!), der um 450 v. Chr. lebte.
(Manchmal werden sie auch als die Möndchen von Alhazen bezeichnet,
benannt nach einem arabischen Mathematiker des 10. und 11. Jahrhunderts.)
Wird der große Halbkreis über der Hypotenuse nach oben geklappt,
dann erscheinen zwei Kreissegmente (Ax und Ay), die mit den Halbkreisen überlappen.
Eliminiert man diese zwei Kreissegmente, so erhält man zwei Möndchen (Ax1 und Ay2),
die dieselbe Fläche besitzen wie das rechtwinklige Dreieck ABC.
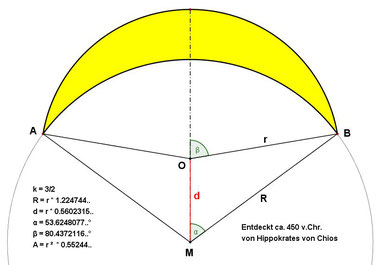
4.) Die nächste Abbildung zeigt einen Sonderfall:
Wenn das rechtwinklige Dreieck zudem gleichschenklig ist,
dann hat ein Möndchen dieselbe Fläche wie das Dreieck AMC.
Dieses Möndchen kann deshalb in ein Quadrat umgeformt werden,
und das allein mit Zirkel und Lineal (ohne Maßstab).
Im weiteren Verlauf wird diese Möglichkeit der Umformung als "quadrierbar" bezeichnet.
Es gibt exakt fünf quadrierbare Möndchen.
(Weitere Informationen dazu siehe unten).
Zunächst beziehen wir uns aber immer auf die einfachste Form
eines quadrierbaren Möndchens wie in dieser Abbildung gezeigt.
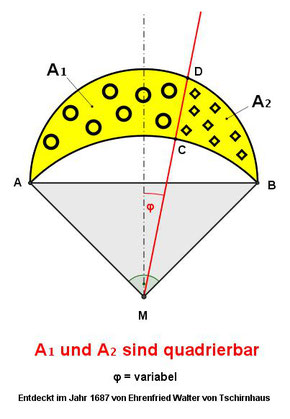
5.) Tschirnhaus entdeckte im Jahr 1687 das folgende Phänomen:
Man kann eine beliebige Linie durch den Mittelpunkt M ziehen
und dabei das Möndchen in zwei Teile teilen.
Diese beiden Teile sind ebenfalls quadrierbar.
Folglich lässt sich das Möndchen in unendlich viele quadrierbare Teile zerlegen.
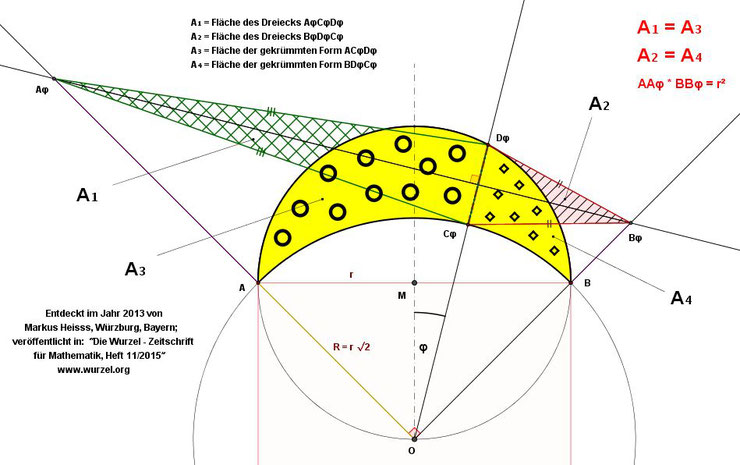
6.) Heisss [sic!] entdeckte im Jahr 2013 eine einfache Methode,
wie man diese beiden Möndchen-Teile konstruktiv quadrieren kann.
7.) Eine weitere bemerkenswerte Entdeckung von Heisss im Jahr 2013
war eine Figur, die wie ein Windrad aussieht.
Man kann zwei verschiedene Formen von Möndchen-Fragmenten sehen,
die dieselbe Fläche haben!
Beide sind deshalb leicht quadrierbar.
8.) Es ist möglich, zwei oder mehrere Möndchen der richtigen Größe zusammenzulegen.
Wenn man acht Möndchen auf diese Weise zusammenlegt,
enthält man eine Figur, die an ein gewundenes Schneckenhaus erinnert.
Die acht Möndchen-Fragmente füllen einen 360°-Winkel im Punkt B.
Schließlich erhält man als Restfläche einen gekrümmten, quadrierbaren Keil mit 0°,
der dem Keil aus der nachfolgenden Abbildung ziemlich ähnlich sieht.
9.) Der gekrümmte Keil GCF kann ebenfalls sehr leicht quadriert werden.
10.) Nikolai Chebotaryov und Anatoly Dorodnov bewiesen im Jahr 1947,
dass es genau fünf quadrierbare Möndchen gibt.
Drei wurden von Hippokrates selbst entdeckt,
und die letzten beiden wurden im Jahr 1766 von Martin Johan Wallenius gefunden,
und im Jahr 1840 von Thomas Clausen wiederentdeckt.
Der Vollständigkeit halber seien nun alle fünf quadrierbaren Möndchen
samt ihrer wichtigsten Kenngrößen aufgeführt,
und im Anschluss daran folgen die Formeln:
11.) Natürlich ist es auch möglich, Bruchstücke dieser Möndchen zu quadrieren:
Man teile die beiden Kreisbögen in eine gleiche Anzahl von Abschnitten
und verbinde die Punkte miteinander (... wie unten gezeigt).
Nur leider versagt die elegante Quadrierungsmethode von Heisss bei den anderen vier Möndchen,
da sich die (roten) Linien nicht in einem gemeinsamen Punkt schneiden!
12.) Ich hoffe, die Seite hat Ihnen gefallen.
Noch mehr interessante Beziehungen zu den Möndchen? ==> [hier]
Referenzen und weitere Informationen:
-
Buch: ==> Thomas Heath: "A History of Greek Mathematics", Volume I, S. 200, Dover Publications, 1981
-
Website: https://markus-heisss.jimdofree.com/geometrie-handskizzen/
- Website: https://en.wikipedia.org/wiki/Lune_of_Hippocrates
-
Magazin: "Die Wurzel – Zeitschrift für Mathematik": Artikel "Die Begradigung eines Möndchens" in Heft 11/2015, S. 234, und "Aufgabe 22" in Heft 5/2017, S. 119 ==> www.wurzel.org
-
Website: http://www.gogeometry.com/school-college/4/p1335-squaring-circle-kite-lune-mobile-apps.htm
- Website: http://www.walser-h-m.ch/hans/Miniaturen/M/Moendchen2/Moendchen2.htm
- Website: https://sss-geometrie.jimdofree.com/m%C3%B6ndchen-des-hippokrates-2/